Giải đề thi học kì 1 lý lớp 11 năm 2020 – 2021 trường THPT Bố Hạ>

Đề bài

A. PHẦN TRẮC NGHIỆM (5 điểm)

Câu 1: Ở 200C điện trở suất của bạc là \(1,{62.10^{ – 8}}\Omega m\). Hệ số nhiệt điện trở của bạc là \(4,{1.10^{ – 3}}{K^{ – 1}}\). Ở 330K thì điện trở suất của bạc là:

A. \(1,{866.10^{ – 8}}\Omega .m\)

B. \(3,{697.10^{ – 8}}\Omega .m\)

C. \(3,{812.10^{ – 8}}\Omega .m\)

D. \(4,{151.10^{ – 8}}\Omega .m\)

Câu 2: Điều kiện để có dòng điện là:

A. có nguồn điện

B. có điện tích tự do

C. có hiệu điện thế

D. có hiệu điện thế và điện tích tự do

Câu 3: Khi đốt nóng chất khí, nó trở lên dẫn điện vì

A. vận tốc giữa các phân tử chất khí tăng

B. khoảng cách giữa các phân tử chất khí tăng

C. chất khí chuyển động thành dòng có hướng

D. các phân tử chất khí bị ion hóa thành các hạt mang điện tự do

Câu 4: Suất điện động của một cặp nhiệt điện phụ thuộc vào

A. hiệu nhiệt độ hai đầu cặp

B. nhiệt độ cao hơn ở một trong hai đầu cặp

C. nhiệt độ thấp hơn ở một trong hai đầu cặp

D. bản chất của chỉ một trong hai kim loại cấu tạo nên cặp

Câu 5: Khi vật dẫn ở trạng thái siêu dẫn, điện trở của nó

A. bằng không

B. có giá trị âm

C. vô cùng lớn

D. có giá trị xác định

Câu 6: Cho dòng điện có cường độ 2A chạy qua bình điện phân đựng dung dịch muối đồng có cực dương bằng đồng trong 1 giờ 4 phút 20 giây. Biết khối lượng mol của đồng là 64g/mol, đồng có hóa trị 2. Khối lượng đồng bám vào cực âm là

A. 2,65 g                     B. 6,25 g

C. 2,56 g                     D. 5,62 g

Câu 7: Lớp vỏ của nguyên tử hidro có 1 electron. Nếu nguyên hidro bị mất hết electron thì nó mang điện tích là

A. \( + 1,{6.10^{ – 19}}C\)      B. \( – 1,{6.10^{ – 19}}C\)

C. \( + 3,{2.10^{ – 19}}C\)      D. \( – 3,{2.10^{ – 19}}C\)

Câu 8: Hai điện tích điểm đặt gần nhau, nếu giảm khoảng cách giữa chúng đi 2 lần thì lực tương tác giữa chúng sẽ

A. tăng lên 2 lần

B. giảm đi 4 lần

C. tăng lên 4 lần

D. giảm đi 2 lần

Câu 9: Đơn vị của điện thế trong hệ SI là

A. N (Niuton)             B. J (Jun)

C. V (Vôn)                  D. m (mét)

Câu 10: Cho đoạn mạch điện trở \(10\Omega \), hiệu điện thế 2 đầu mạch là 20V. Điện năng đoạn mạch tiêu thụ trong 1 giờ là

A. 2,4 kJ                      B. 144 kJ

C. 120 J                       D. 40 J

Câu 11: Cho đoạn mạch như hình vẽ (H.1) trong đó \({E_1} = 9V,{r_1} = 1,2\Omega ;{E_2} = 3V,{r_2} = 0,4\Omega \); điện trở \(R = 28,4\Omega \). Hiệu điện thế giữa hai đầu đoạn mạch \({U_{AB}} = 6V\). Dòng điện chạy qua đoạn mạch có

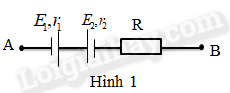
A. chiều từ A sang B, độ lớn 0,4A

B. chiều từ B sang A, độ lớn 0,4A

C. chiều từ A sang B, độ lớn 0,6A

D. chiều từ B sang A, độ lớn 0,6A

Câu 12: Khi nói về chất điện môi, phát biểu nào sau đây không đúng?

A. Hằng số điện môi của một môi trường xác định là hằng số

B. Điện môi là môi trường cách điện

C. Hằng số điện môi có thể nhỏ hơn 1

D. Hằng số điện môi của chân không bằng 1

Câu 13: Công của lực điện trường dịch chuyển một điện tích \(1\mu C\) dọc theo chiều một đường sức trong một điện trường đều 1000 V/m trên quãng đường dài 1m là

A. 1 J                           B. 1 mJ

C. 1000 J                     D. \(1\mu J\)

Câu 14: Một electron được thả không vận tốc ban đầu ở sát bản âm trong điện trường đều giữa hai bản kim loại phẳng tích điện trái dấu. Cường độ điện trường giữa hai bản là 100 V/m. Khoảng cách giữa hai bản là 1cm. Động năng của electron khi nó đến đập vào bản dương là

A. \(1,{6.10^{ – 17}}J\)   B. \(1,{6.10^{ – 19}}J\)          

C. \(1,{6.10^{ – 20}}J\)   D. \(1,{6.10^{ – 18}}J\)

Câu 15: Điện năng tiêu thụ được đo bằng dụng cụ nào sau đây?

A. Tĩnh điện kế           B. Vôn kế

C. Ampe kế                 D. Công tơ điện

Câu 16: Hiện tượng điện phân không ứng dụng để

A. đúc điện                  B. mạ điện

C. sơn tĩnh điện          D. luyện nhôm

Câu 17: Để bóng đèn loại 120V – 60W sáng bình thường, người ta phải mắc bóng đèn đó ở mạng điện có hiệu điện thế là

A. 20 V                       B. 120 V

C. 60 V                       D. 100 V

Câu 18: Trên vỏ một tụ điện có ghi \(20\mu F\), số liệu đó cho biết

A. điện dung của tụ

B. điện tích cực đại của tụ

C. hiệu điện thế hai đầu tụ

D. điện tích của tụ

Câu 19: Một mạch điện kín gồm hai nguồn điện \({\xi _1},{r_1}\) và \({\xi _2},{r_2}\) mắc nối tiếp với nhau, mạch ngoài chỉ có điện trở R. Biểu thức cường độ dòng điện chạy trong mạch được tính theo công thức là

A. \(I = \frac{{{\xi _1} – {\xi _2}}}{{R + {r_1} – {r_2}}}\)

B. \(I = \frac{{{\xi _1} – {\xi _2}}}{{R + {r_1} + {r_2}}}\)

C. \(I = \frac{{{\xi _1} + {\xi _2}}}{{R + {r_1} – {r_2}}}\)

D. \(I = \frac{{{\xi _1} + {\xi _2}}}{{R + {r_1} + {r_2}}}\)

Câu 20: Một dòng điện không đổi, sau 1 phút có một điện lượng 24 C chuyển qua một tiết diện thẳng. Cường độ của dòng điện đó là

A. 24A                        B. 2,4A

C. 0,2A                       D. 0,4A

B. PHẦN TỰ LUẬN (5,0 điểm)

Bài 1 (2,5 điểm): Trong chân không đặt điện tích điểm \({q_1} =  + {4.10^{ – 8}}C\) tại điểm O. Xét điểm M cách O một đoạn 2cm.

a ) Tính cường độ điện trường tại điểm M .
b ) Tại M đặt một điện tích điểm q2. Lực điện giữa hai điện tích là lực hút, có độ lớn là 0,018 N. Tìm dấu và độ lớn của điện tích q2 .
c ) Điện tích \ ( { q_3 } = { 8.10 ^ { – 8 } } C \ ) đặt tại M. Xác định cường độ điện trường tại điểm N cách O 2 cmvà cách M 4 cm .

Bài 2 (2,5 điểm): Cho mạch điện gồm điện trở \({R_1} = 4\Omega \), đèn ghi 6V – 9W, biến trở \({R_b} = 1,5\Omega \). Nguồn điện có suất điện động 12V, điện trở trong \(2,5\Omega \). Các dụng cụ trên được mắc như hình vẽ (H.2).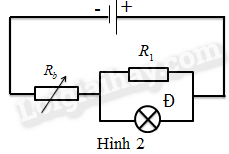

a ) Tính cường độ dòng điện chạy trong mạch chính .
b ) Độ sáng của đèn lúc này như thế nào ?
c ) Thay đổi giá trị của biến trở để hiệu suất tiêu thụ của mạch ngoài đạt cực lớn. Khi đó, \ ( { R_b } \ ) phải có giá trị bằng bao nhiêu ? Tính hiệu suất tiêu thụ của mạch lúc này.

Lời giải chi tiết

HƯỚNG DẪN GIẢI CHI TIẾT

Thực hiện: Ban chuyên môn Loigiaihay.com

A. PHẦN TRẮC NGHIỆM

1. A

2. D

3. D

4. A

5. A

6. C

7. A

8. C

9. C

10. B

11. A

12. C

13. B

14. D

15. D

16. C

17. B

18. A

19. D

20. D

Câu 1:

Phương pháp

Sử dụng công thức phụ thuộc vào của điện trở suất của sắt kẽm kim loại theo nhiệt độ :\ ( \ rho = { \ rho _0 } \ left [ { 1 + \ alpha \ left ( { t – { t_0 } } \ right ) } \ right ] \ )

Cách giải

Theo đề bài ta có : \ ( \ left \ { \ begin { array } { l } { t_0 } = { 20 ^ 0 } C \ \ t = 330 – 273 = { 57 ^ 0 } C \ end { array } \ right. \ )Điện trở suất của bạc ở 330K là :\ ( \ begin { array } { l } \ rho = { \ rho _0 } \ left [ { 1 + \ alpha \ left ( { t – { t_0 } } \ right ) } \ right ] \ \ = 1, { 62.10 ^ { – 8 } } \ left [ { 1 + 4, { { 1.10 } ^ { – 3 } } \ left ( { 57 – 20 } \ right ) } \ right ] \ \ = 1, { 866.10 ^ { – 8 } } \ left ( { \ Omega m } \ right ) \ end { array } \ )

Chọn A

Câu 2:

Phương pháp

Vận dụng triết lý về điều kiện kèm theo để có dòng điện :- Các vật cho dòng điện chạy qua được gọi là vật dẫn. Các hạt mang điện trong những vật dẫn có đặc thù là hoàn toàn có thể dịch chuyển tự do .- Phải có hiệu điện thế giữa hai đầu một đoạn mạch hay giữa hai đầu một bóng đèn .

Cách giải

Điều kiện để có dòng điện là có hiệu điện thế và điện tích tự do .

Chọn D

Câu 3:

Phương pháp

Vận dụng triết lý về thực chất của dòng điện trong chất khí :Dòng điện trong chất khí là dòng chuyển dời có hướng của những ion dương theo chiều điện trường và những ion âm, những electron ngược chiều điện trường. Các hạt tải điện này do chất khí bị ion hóa sinh ra .

Cách giải

Khi đốt nóng chất khí, nó trở nên dẫn điện vì những phân tử chất khí bị ion hóa thành những hạt mang điện tự do .

Chọn D

Câu 4:

Phương pháp

Sử dụng biểu thức của suất điện động nhiệt điện :\ ( \ xi = { \ alpha _t } \ left ( { { T_1 } – { T_2 } } \ right ) \ )

Cách giải

Ta có : \ ( \ xi = { \ alpha _t } \ left ( { { T_1 } – { T_2 } } \ right ) \ ) => Nó nhờ vào vào hiệu nhiệt độ hai đầu cặp .

Chọn A

Câu 5:

Phương pháp

Vận dụng triết lý điện trở của sắt kẽm kim loại ở nhiệt độ thấp :Một số sắt kẽm kim loại và kim loại tổng hợp, khi nhiệt độ thấp hơn một nhiệt độ tới hạn Tc thì điện trở suất bất ngờ đột ngột giảm xuống bằng 0. Ta nói những vật tư ấy đã chuyển sang trạng thái siêu dẫn .

Cách giải

Khi vật dẫn ở trạng thái siêu dẫn, điện trở của nó bằng 0 .

Chọn A

Câu 6:

Phương pháp

Vận dụng biểu thức định luật Faraday thứ hai :\ ( m = \ frac { 1 } { F }. \ frac { { AIt } } { n } \ )

Cách giải

Đổi 1 giờ 4 phút 20 giây = 3860 giâyKhối lượng đồng bám vào cực âm là :\ ( m = \ frac { 1 } { F }. \ frac { { AIt } } { n } = \ frac { 1 } { { 96500 } }. \ frac { { 64.2.3860 } } { 2 } = 2,56 g \ )

Chọn C

Câu 7:

Phương pháp

Cách giải

Nguyên tử hidro mất hết electron thì nó mang điện tích là :\ ( 1.1, { 6.10 ^ { – 19 } } = + 1, { 6.10 ^ { – 19 } } C \ )

Chọn A

Câu 8:

Phương pháp

Vận dụng biểu thức định luật Culông : \ ( F = k \ frac { { \ left | { { q_1 } { q_2 } } \ right | } } { { \ varepsilon { r ^ 2 } } } \ )

Cách giải

Ta có : \ ( \ left \ { \ begin { array } { l } { F_1 } = k \ frac { { \ left | { { q_1 } { q_2 } } \ right | } } { { \ varepsilon { r ^ 2 } } } \ \ { F_2 } = k \ frac { { \ left | { { q_1 } { q_2 } } \ right | } } { { \ varepsilon { { \ left ( { \ frac { r } { 2 } } \ right ) } ^ 2 } } } = 4. k \ frac { { \ left | { { q_1 } { q_2 } } \ right | } } { { \ varepsilon { r ^ 2 } } } \ end { array } \ right. \ )\ ( \ Rightarrow { F_2 } = 4 { F_1 } \ )

Chọn C

Câu 9:

Phương pháp

Vận dụng kim chỉ nan về điện thế .

Cách giải

Đơn vị của điện thế trong hệ SI là Vôn ( V ) .

Chọn C

Câu 10:

Phương pháp

Sử dụng công thức tính điện năng tiêu thụ : A = UIt

Cách giải

Cường độ dòng điện chạy qua đoạn mạch là :

\ ( I = \ frac { U } { R } = \ frac { { 20 } } { { 10 } } = 2 { \ rm { A } } \ )Điện năng đoạn mạch tiêu thụ trong 1 giờ là :\ ( A = UIt = 20.2.1 = 40 \ left ( { { \ rm { W } } h } \ right ) = 144000J = 144 kJ \ )

Chọn B

Câu 11:

Phương pháp

Vận dụng định luật Ôm cho đoạn mạch chứa cả máy thu và nguồn điện ( máy phát ) :\ ( I = \ frac { { { U_ { AB } } + { E_p } – { E_t } } } { { R + { r_p } + { r_t } } } \ )+ Đối với nguồn điện ( máy phát ) : dòng điện đi vào cực âm và đi ra từ cực dương .+ Đối với máy thu : dòng điện đi vào cực dương và đi ra từ cực âm .

Cách giải

Giả sử dòng điện có chiều từ A đến B. Khi đó E1 là máy phát, E2 là máy thu .Áp dụng định luật Ôm cho đoạn mạch AB ta có :\ ( I = \ frac { { { U_ { AB } } + { E_1 } – { E_2 } } } { { R + { r_1 } + { r_2 } } } = \ frac { { 6 + 9 – 3 } } { { 28,4 + 1,2 + 0,4 } } = 0,4 \ )Ta thấy I > 0 => Điều giả sử là đúng .Vậy dòng điện có chiều từ A đến B, có độ lớn là 0,4 A .

Chọn A

Câu 12:

Phương pháp

Vận dụng kim chỉ nan về hằng số điện môi .

Cách giải

– Điện môi là một thiên nhiên và môi trường cách điện .- Hằng số điện môi \ ( \ varepsilon \ ge 1 \ )- Đối với chân không \ ( \ varepsilon = 1 \ ), còn so với những thiên nhiên và môi trường khác \ ( \ varepsilon > 1 \ )=> Hằng số điện môi không hề nhỏ hơn 1 .

Chọn C

Câu 13:

Phương pháp

Sử dụng công thức tính công : A = qEd

Cách giải

Công của lực điện trường là :\ ( A = qEd = { 10 ^ { – 6 } }. 1000.1 = { 10 ^ { – 3 } } \ left ( J \ right ) = 1 mJ \ )

Chọn B

Câu 14:

Phương pháp

Công của lực điện trường bằng độ biến thiên động năng :\ ( A = \ Delta { { \ rm { W } } _d } = { { \ rm { W } } _ { d2 } } – { { \ rm { W } } _ { d1 } } \ )

Cách giải

Lực điện trường F công dụng lên electron ( điện tích âm ) có chiều ngược với chiều điện trường => electron chuyển dời ngược chiều điện trường => \ ( \ left ( { \ overrightarrow E, \ overrightarrow s } \ right ) = { 180 ^ 0 } \ )

Áp dụng định lý động năng cho sự chuyển dời của electron :\ ( { { \ rm { W } } _ { d ( + ) } } – { { \ rm { W } } _ { d ( – ) } } = A = qEs. \ cos { 180 ^ 0 } \ )Electron được thả không tốc độ đầu => động năng bắt đầu tại bản âm \ ( { { \ rm { W } } _ { d ( – ) } } = 0 \ )Động năng của electron khi nó đến đập vào bản dương là :\ ( \ begin { array } { l } { { \ rm { W } } _ { d ( + ) } } = qEs. \ cos { 180 ^ 0 } \ \ = – 1, { 6.10 ^ { – 19 } }. 1000.0,01. \ left ( { – 1 } \ right ) \ \ = 1, { 6.10 ^ { – 18 } } J \ end { array } \ )

Chọn D

Câu 15:

Phương pháp

Điện năng tiêu thụ được đo bằng công tơ điện .

Cách giải

Điện năng tiêu thụ được đo bằng công tơ điện .

Chọn D

Câu 16:

Phương pháp

Vận dụng triết lý về ứng dụng của hiện tượng kỳ lạ điện phân :- Điều chế hóa chất : điều chế clo, hidro, xút trong công nghiệp hóa chất .- Luyện kim : những sắt kẽm kim loại như đồng, nhôm, magiê và nhiều hóa chất được điều chế trực tiếp bằng chiêu thức điện phân .

– Mạ điện .

Cách giải

Sơn tĩnh điện không phải là ứng dụng của hiện tượng kỳ lạ điện phân. Nó là ứng dụng của lực Culông, khi đó sơn và vật cần sơn sẽ được tích điện trái dấu làm sơn sẽ bám chặt vào vật cần sơn .

Chọn C

Câu 17:

Phương pháp

Để bóng đèn sáng thông thường thì \ ( U = { U_ { dm } } \ )

Cách giải

Để bóng đèn sáng thông thường thì \ ( U = { U_ { dm } } = 120V \ )

Chọn B

Câu 18:

Phương pháp

Vận dụng triết lý về tụ điện .

Cách giải

Trên vỏ một tụ điện có ghi \ ( 20 \ mu F \ ), số liệu đó cho biết điện dung của tụ .

Chọn A

Câu 19:

Phương pháp

– Vận dụng công thức của bộ nguồn tiếp nối đuôi nhau .- Vận dụng biểu thức của định luật Ôm .

Cách giải

Suất điện động và điện trở trong của bộ là : \ ( \ left \ { \ begin { array } { l } { \ xi _b } = { \ xi _1 } + { \ xi _2 } \ \ { r_b } = { r_1 } + { r_2 } \ end { array } \ right. \ )Cường độ dòng điện chạy trong mạch là :\ ( I = \ frac { { { \ xi _b } } } { { R + { r_b } } } = \ frac { { { \ xi _1 } + { \ xi _2 } } } { { R + { r_1 } + { r_2 } } } \ )

Chọn D

Câu 20:

Phương pháp

Sử dụng công thức \ ( I = \ frac { q } { t } \ )

Cách giải

Cường độ dòng điện là :\ ( I = \ frac { q } { t } = \ frac { { 24 } } { { 60 } } = 0,4 A \ )

Chọn D

B. PHẦN TỰ LUẬN

Câu 1:

Phương pháp

Sử dụng công thức tính cường độ điện trường : \ ( E = k \ frac { { \ left | q \ right | } } { { \ varepsilon { r ^ 2 } } } \ )Sử dụng biểu thức định luật Culông : \ ( F = k \ frac { { \ left | { { q_1 } { q_2 } } \ right | } } { { \ varepsilon { r ^ 2 } } } \ )Sử dụng nguyên tắc chồng chất điện trường : \ ( \ overrightarrow E = \ overrightarrow { { E_1 } } + \ overrightarrow { { E_2 } } + … \ )

Cách giải

a )Cường độ điện trường tại M là :\ ( E = k \ frac { { \ left | q \ right | } } { { { r ^ 2 } } } = { 9.10 ^ 9 }. \ frac { { { { 4.10 } ^ { – 8 } } } } { { 0, { { 02 } ^ 2 } } } = { 9.10 ^ 5 } \ left ( { V / m } \ right ) \ )b )Do lực điện giữa hai điện tích là lực hút nên \ ( { q_2 } \ ) là điện tích âm .Ta có :\ ( \ begin { array } { l } F = k \ frac { { \ left | { { q_1 }. { q_2 } } \ right | } } { { \ varepsilon { r ^ 2 } } } = 0,018 \ \ \ Leftrightarrow { 9.10 ^ 9 }. \ frac { { \ left | { { { 4.10 } ^ { – 8 } }. { q_2 } } \ right | } } { { 0, { { 02 } ^ 2 } } } = 0,018 \ \ \ Leftrightarrow \ left | { { q_2 } } \ right | = { 2.10 ^ { – 8 } } \ end { array } \ )

Vậy \ ( { q_2 } = – { 2.10 ^ { – 8 } } C \ )c )Ta có : \ ( \ left \ { \ begin { array } { l } NO = 2 cm \ \ NM = 4 cm \ \ MO = 2 cm \ end { array } \ right. \ Rightarrow NO + MO = \ frac { { MN } } { 2 } \ )Suy ra O là trung điểm của MN .

Ta màn biểu diễn được những vecto cường độ điện trường \ ( \ overrightarrow { { E_1 } }, \ overrightarrow { { E_3 } } \ ) do điện tích \ ( { q_1 }, { q_3 } \ ) gây ra tại điểm N có phương và chiều như hình vẽ .Ta có :\ ( { E_1 } = k \ frac { { \ left | { { q_1 } } \ right | } } { { N { O ^ 2 } } } = { 9.10 ^ 9 }. \ frac { { { { 4.10 } ^ { – 8 } } } } { { 0, { { 02 } ^ 2 } } } = { 9.10 ^ 5 } V / m \ )\ ( { E_3 } = k \ frac { { \ left | { { q_3 } } \ right | } } { { N { M ^ 2 } } } = { 9.10 ^ 9 }. \ frac { { { { 8.10 } ^ { – 8 } } } } { { 0, { { 04 } ^ 2 } } } = 4, { 5.10 ^ 5 } V / m \ )Cường độ điện trường tại N là :\ ( { E_N } = { E_1 } + { E_3 } = \ left ( { 9 + 4,5 } \ right ) {. 10 ^ 5 } = 13, { 5.10 ^ 5 } \ left ( { V / m } \ right ) \ )

Câu 2:

Phương pháp

– Vận dụng biểu thức định luật Ôm cho toàn mạch : \ ( I = \ frac { E } { { { R_N } + r } } \ )

– Sử dụng công thức tính hiệu suất tiêu thụ : \ ( P = UI = \ frac { { { U ^ 2 } } } { R } = { I ^ 2 } R \ )- Áp dụng bất đẳng thức côsi .

Cách giải

a )Điện trở của bóng đèn là :\ ( { R_D } = \ frac { { { U ^ 2 } } } { P } = \ frac { { { 6 ^ 2 } } } { 9 } = 4 \ left ( \ Omega \ right ) \ )Điện trở mạch ngoài là :\ ( { R_N } = { R_b } + \ frac { { { R_1 }. { R_D } } } { { { R_1 } + { R_D } } } = 1,5 + \ frac { { 4.4 } } { { 4 + 4 } } = 3,5 \ left ( \ Omega \ right ) \ )Cường độ dòng điện chạy trong mạch chính là :\ ( I = \ frac { E } { { { R_N } + r } } = \ frac { { 12 } } { { 3,5 + 2,5 } } = 2A \ )b )Cường độ dòng điện để đèn sáng thông thường là :\ ( { I_ { dm } } = \ frac { U } { { { R_D } } } = \ frac { 6 } { 2 } = 3 { \ rm { A } } \ )Ta thấy \ ( I < { I_ { dm } } \ ) nên độ sáng lúc này của đèn tối hơn thông thường .c )Công suất tiêu thụ của mạch ngoài là :\ ( P = { I ^ 2 } { R_N } = \ frac { { { E ^ 2 } } } { { { { \ left ( { { R_b } + \ frac { { { R_1 }. { R_D } } } { { { R_1 } + { R_D } } } + r } \ right ) } ^ 2 } } }. \ left ( { { R_b } + \ frac { { { R_1 }. { R_D } } } { { { R_1 } + { R_D } } } } \ right ) \ ) \ ( P = \ frac { { { E ^ 2 } } } { { { { \ left ( { { R_b } + 2 + r } \ right ) } ^ 2 } } } \ left ( { { R_b } + 2 } \ right ) \ )Chia cả tử và mẫu cho \ ( \ left ( { { R_b } + 2 } \ right ) \ ) ta được :\ ( P = \ frac { E } { { { { \ left ( { \ sqrt { { R_b } + 2 } + \ frac { r } { { \ sqrt { { R_b } + 2 } } } } \ right ) } ^ 2 } } } \ )P. max khi \ ( \ left ( { \ sqrt { { R_b } + 2 } + \ frac { r } { { \ sqrt { { R_b } + 2 } } } } \ right ) \ min \ )Áp dụng bất đẳng thức cô-si cho hai số dương \ ( \ sqrt { { R_b } + 2 } \ ) và \ ( \ frac { r } { { \ sqrt { { R_b } + 2 } } } \ ) ta được :\ ( \ left ( { \ sqrt { { R_b } + 2 } + \ frac { r } { { \ sqrt { { R_b } + 2 } } } } \ right ) \ ge 2 \ sqrt { \ left ( { \ sqrt { { R_b } + 2 }. \ frac { r } { { \ sqrt { { R_b } + 2 } } } } \ right ) } \ )Dấu “ = ” xảy ra khi \ ( \ sqrt { { R_b } + 2 } = \ frac { r } { { \ sqrt { { R_b } + 2 } } } \ Leftrightarrow { R_b } + 2 = r \ )Suy ra \ ( { R_b } = r - 2 = 2,5 - 2 = 0,5 \ Omega \ )

Vậy P max khi \({R_b} = 0,5\Omega \).

Công suất tiêu thụ mạch ngoài cực lớn là :\ ( { P_ { \ max } } = \ frac { { { { 12 } ^ 2 } } } { { { { \ left ( { 0,5 + 2 + 2,5 } \ right ) } ^ 2 } } }. \ left ( { 0,5 + 2 } \ right ) = 14,4 { \ rm { W } } \ )

Loigiaihay.com

Source: https://baoduongdieuhoa24h.com
Category: Điện Tử